前段时间 刷讲座课学分 有幸参加了微众银行(WeBank)的范力欣博士与康焱博士的讲座“联邦学习:目的、方法及应用”,对其中提到的Passport方法感到好奇,因此对相关论文进行了阅读,并在组会上进行了分享。在此对组会上的PPT内容进行整理记录。
背景
联邦学习是一种在保护数据隐私的前提下,通过各方合作训练深度学习模型来充分发挥各方数据的价值的方法。因其在安全且充分利用各方数据资源方面的作用而受到广泛关注。
但是,面对包含大量参数的深度学习模型,当前联邦学习中运用的隐私保护方案存在各种问题。
- 模型准确率低
- 隐私保护性不高
- 模型收敛速度慢,计算、通信开销大
这三个方向的问题,实际上构成了联邦学习中的一组不可能三角,即单一隐私保护方案难以在三方面都有完美表现。
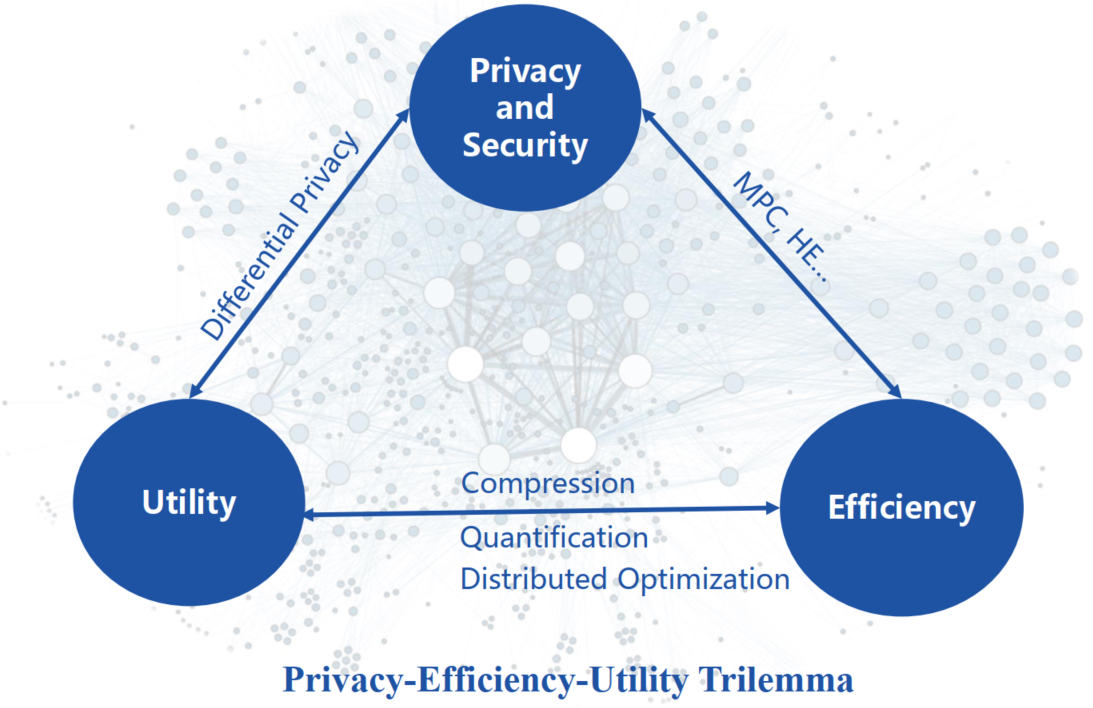
在这种背景下,作者希望寻求一种能够在三方面都有不错表现的隐私保护方案。
相关工作
本文从三个方面对相关工作进行了总结归纳,包括隐私定义、隐私保护机制与隐私泄露攻击,其中对前两个方面的总结归纳比较到位。
隐私定义
-
$(\epsilon,\delta)-$差分隐私(Differential Privacy):
$\qquad$一个算法被认为满足$(\epsilon,\delta)-$差分隐私,当且仅当对于两个相距为1的数据集$S,S^\prime$,对于任意的输出集合$E$,应该有
$$\mathbb{P}(M(S)\in E)\leq e^\epsilon\mathbb{P}(M(S^\prime)\in E)+\delta.$$
这种隐私性定义方式提出较久,且较为严密,被较为广泛地接受,有较多基于该方式的后续工作。
-
贝叶斯隐私(Baysian Privacy):
$\qquad$贝叶斯隐私计算攻击者对数据的先验分布与其通过暴露的公开信息恢复出的数据后验分布之间的KL散度(Kullback-Leibler divergence),分析两分布之间的差异,以衡量隐私数据的泄露程度。
隐私保护机制
-
基于随机加噪的保护机制
$\qquad$通过随机噪声的引入对交换的数据进行扰动,以达到保护隐私数据的目的。运算较为简单,受到较大关注,但不可避免地带来模型训练收敛速度较慢、最终模型准确率不高以及隐私保护能力不强等问题。
-
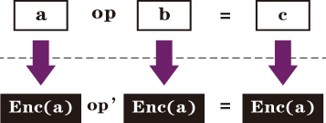
基于同态加密的保护机制
$\qquad$通过算法设计,使得基于密文的计算在解密后的结果与直接基于明文的计算结果相同。能够很好地保证安全性,但计算和通信开销较高。
-
基于拆分学习的保护机制
$\qquad$将模型拆分为公有部分和私有部分。中心服务器只对公有模型部分进行参数的聚合与分发,通过对于私有模型的隐藏来保证安全性。但实验表明,进攻者仍然可以通过参与方暴露给中心服务器的数据来推断出私有模型数据。
-
基于Passport层的保护机制
$\qquad$对一个卷积层嵌入passport的方法如图。正常的卷积操作只有左边部分。而嵌入passport后,事先设定的参数$p_γ^l、p_β^l$同样经过卷积层,再经过编码器、解码器池化层之后分别得到参数γ、β用于对正常输出进行伸缩和偏移变换。
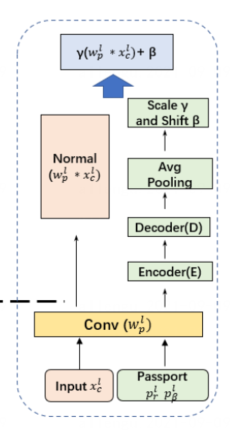
$\qquad$该方法实际上不是作为一个隐私保护方案被提出的,而是为了调节模型输出,以达到验证模型所有权及知识产权的目的。根据前作的解释,passport层的引入是为了给伸缩参数γ、偏移参数β与网络的权重之间引入相关性,使得当输入非法passport时,模型的结果将产生较大偏差。这里参数$p_γ^l、p_β^l$的作用类似于密码学中的私钥。
贝叶斯隐私
本文基于贝叶斯隐私框架对隐私保护与攻击两类对抗策略进行了较为深入的形式化分析,这也是本文在写作上比较值得借鉴的地方。
问题假定
- 多组织通过横向联邦学习共同进行模型训练DNN模型。
- 某些参与方(或中央服务器)是半诚实的,即不会提交错误数据或恶意执行错误计算,但可能利用联邦学习过程中交换的信息对其他参与方进行隐私攻击。
- 单个参与方拥有隐私数据 $x$,并会暴露公共数据 $G$,此处 $G$ 与 $x$ 相关,满足映射 $G=g(x)$。需要注意的是,在联邦学习中,映射 $g()$ 被所有参与方知晓,因为其训练的模型结构是相同的。但隐私数据 $x$ 仅被参与方自身了解。
- 分类任务中 G的计算通过最小化损失函数来完成。
- 半诚实参与方会试图通过最小化 $|g(\widetilde x)-G|$,以达到用 $\widetilde x$ 来估计 $x$ 的目的。
在上述问题假定下,存在两方相互对抗的机制。即隐私数据保护机制 $M$ 与隐私攻击机制 $A$。
联邦学习中的隐私保护机制
本文将该情境下隐私保护机制定义为映射
$$\widetilde{G}=M(G),$$
将参与方暴露的公共信息 $G$ 作为输入,输出一个修改过的公共信息 $G$。具体修改方式与隐私保护机制相关:
- 基于随机噪声的保护机制: $$\widetilde{G}=Rand_\epsilon(G)=G+\epsilon$$
- 基于引入稀疏性的保护机制: $$\widetilde{G}=Spar_{s,t}(G)$$
- 基于调整的保护机制:
$$\widetilde{G}=Mod_P(G)=\mathop{\arg\min}_{G}(L_{CE}(G,x)+L_P(G,P))$$
- 基于同态加密的保护机制: $$\widetilde{G}=Enc(G)$$
值得注意的是,这些隐私保护机制可以进行组合,以提供更高的隐私保护能力。本文中的方法就是对基于引入稀疏性的split learning和基于调整的passport layer方法进行有机结合,最终达到较为满意的效果。
联邦学习中的隐私攻击机制
本文将该情境下隐私保护机制定义为映射 $$\widetilde{x}^*=A(\widetilde{G}):=\mathop{\arg\min}_{\widetilde{x}}L(g(\widetilde{x}),\widetilde{G}),$$ 而基于贝叶斯框架,攻击者根据公开信息来还原数据可表示为 $$P(\widetilde{x}|\widetilde{G})=\frac{P(\widetilde{G}|\widetilde{x})P(\widetilde{x})}{P(\widetilde{G})}\propto P(\widetilde{G}|\widetilde{x})P(\widetilde{x}),$$ 因此,攻击者获得最优恢复数据的过程可表达为
其中,$L_2=-log(P(\widetilde{x}))$ 是在为引入引入先验,例如图像的平滑性带来的先验。而 $L_1=-log(P(\widetilde{G}|\widetilde{x}))$ 则又是根据不同的攻击方式具有不同的具体形式:
-
模型逆向攻击:
$$L_1(g(\widetilde{x}),\widetilde{G})=||\widetilde{O}-O||^2.$$ -
基于梯度的攻击:
$$L_1(g(\widetilde{x}),\widetilde{G})=||\nabla W(\widetilde{O})-\nabla W(O)||^2.$$
从攻击者角度,私有数据的重建实际上是对于私有数据知识的增加。
带有对抗过程的贝叶斯隐私框架
给定隐私保护机制 $M$,隐私泄露攻击 $A$,攻击者对于私有数据 $x$ 的先验分布 $F_0$,本文将贝叶斯隐私定义为
同时,针对攻击者对隐私数据的先验$F_0$的质量,作者进行了分类讨论:
- 攻击者对私有数据几乎没有先验知识,先验接近均匀分布,即$F_0=\bar F$,此时攻击者希望复原的数据能够更贴近真实数据而非随机猜测,因此想要更高的KL散度以获得更高的知识增量;而防御者希望KL散度越低越好,以保证隐私数据的信息不被过多泄露。因此,双方之间的对抗体现为
- 攻击者已经大致了解私有数据的分布情况,先验分布约等于真实分布,即$F_0\approx F^*$。此时,攻击者希望复原的数据尽量服从该分布,因此想要尽量减小KL散度;而防御者则希望增大KL散度来误导攻击者。因此,双方之间的对抗体现为
需要注意的是,此处的攻击与防御措施分别由攻击者与防御者双方来进行,提出的Bayesian privacy框架仅仅是为了更好对两个过程进行综合分析。
基于私有Passport的联邦学习
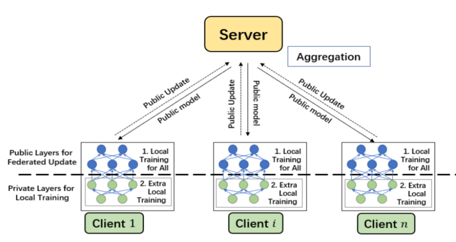
作者综合前述分析,结合了拆分学习与Passport层,提出了基于私有Passport的联邦学习,具体架构如下。
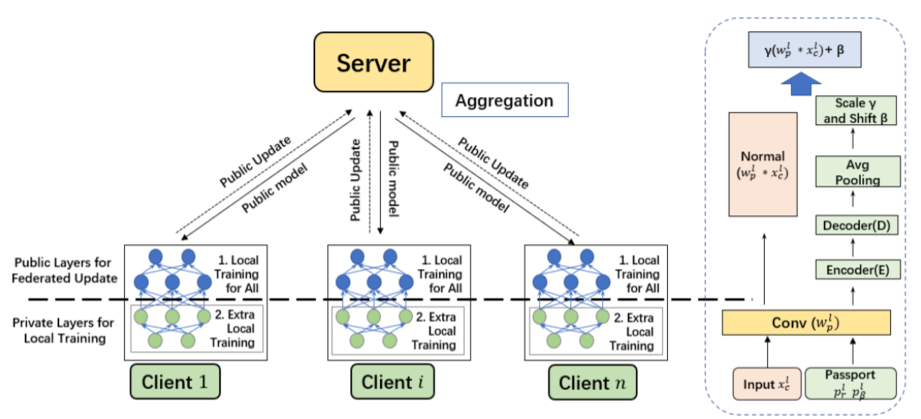
该框架实际上是对split learning和passport layer的结合。 每个client的本地模型分为public和private两部分,只有public部分的模型会参与中心服务器的聚合与分发(如图片左半边所示)。Private模型仅在本地更新。而在private部分的模型中,又嵌入passport层,以进一步保护本地隐私数据的安全性(如图片右半边所示)。
个人理解Passport层的作用是为不同参与方的模型输入分布进行扰动,使得不同参与方所训练的模型存在差异性,因而难以被恶意参与方攻击。

-
训练主体部分1-9,中央服务器分发public模型参数,各客户端获取参数,分别进行本地训练,对public模型权重进行更新并回传给服务器,服务器随后对模型权重进行聚合。
-
client本地训练部分10-16,客户端正常训练,获得loss信息,对public部分进行权重更新。
-
Client本地私有训练部分17-23,冻结public模型的参数,仅根据本地计算的loss对private模型参数进行更新。
理论分析
理论证明过程较为冗长,主要通过证明两个关键命题来表明上述两个方法结合的必要性:
- 在拆分学习中,即便private部分的模型没有被暴露,攻击者依然能够较为容易地复原隐私数据。命题最终给出了贝叶斯隐私的上界:
$$
\begin{aligned}
\sqrt{BP_{MSE}(x,\widetilde{x})}
&=||\widetilde{x}-x||_2\\
&=||W^+\cdot O_1-\widetilde{W}^+\cdot O_2||_2\\
&\leq C_1||\widetilde{W}^+||2||W^+||_2||W-\widetilde{W}||_2 \end{aligned} $$
由该上界表达式可见,在攻击者与隐私数据拥有者之间的获得的权重十分接近的前提下,攻击者能够有效重建隐私数据。作者对此提出一个假定:在没有passport层的情况下,不同参与方之间的private模型通常会学到较为相近的权重。 在该假定为真的情况下,我们根据前述上界知道,攻击者确实能够较为容易地复原隐私数据。
- 嵌入passport层能够有效防止隐私数据被复原。命题最终给出了贝叶斯隐私的下界:
$$
\begin{aligned}
BP_{MSE}(x,\widetilde{x})
&=||\widetilde{x}-x||_2\\
&=||W^+\cdot O_1-\widetilde{W}^+\cdot O_2||_2\\
&\geq \frac{1}{||\widetilde{W}-W||_2}\\
&\geq \frac{1}{||\widetilde{W}||_2+||W||_2}\\
&=\frac{1}{||\widetilde{D}_\gamma\cdot\widetilde{w}||_2+||D_\gamma\cdot w||_2}\\
&\geq \frac{1}{||\widetilde{D}_\gamma||_2||\widetilde{w}||_2+||D_\gamma||_2||w||_2}\\
&\geq \frac{C_2}{||D_\gamma||_2+||\widetilde{D}_\gamma||_2} \end{aligned} $$
作者对该命题又提出两个假定:嵌入passport会使得该下界的分母减小,且会使得模型整体的秩降低。 若这两个假定均为真,则passport层的确可以提高贝叶斯隐私的下界,即提高了整体的隐私保护能力。
在上述两个关键命题的证明过程中,作者利用了三个难以通过理论论证直接证明的假定,在之后的工作中,通过专门设计的实验来对这三个假定进行实践的检验。这种方法在日后的论文写作过程中也十分值得借鉴。
实验
本文中,作者通过实验比较了所提出方法与各传统方法的效果,验证了所提出方法的优越性。
实验条件
- 实验数据集:MNIST, CIFAR10, CIFAR100
- 实验网络:Lenet,Alexnet,Resnet-18
- 对照算法:不加隐私保护的分布式学习(DL)、带差分隐私的联邦学习(DLDP-A、DLDP-B)、拆分学习(SplitFed)。
- FDL-PP设定:第一个卷积层和激活函数设为private,后续层数设为public。在private层之后嵌入passport层。
- 攻击算法:基于梯度的攻击、模型逆向攻击。
- 评价标准:
- 模型效果:准确率
- 训练复杂性:训练时间
- 隐私保护能力:基于前述贝叶斯隐框架的隐私评估
注:此处DLDP-A、DLDP-B分别对应$\sigma=0.002$与$\sigma=0.128$的高斯噪声。且在实验中,基于贝叶斯隐私框架的评估被退化为基于MSE loss的评估体系。
实验结果
作者首先展示了对于两张图片的攻击结果。其中,对于同一张图片,上面一行为基于梯度攻击的结果,下一行为模型逆向攻击的结果。除了直观感受复原前后的图片差距,图片下方还给出了攻击得到的图片与原图片的 MSE loss,便于从数值上体会具体差异大小。

作者接着在下图中给出了各种方式在前述三个数据集以及两种攻击方式下的表现对比。图中横坐标是最终模型的准确率,纵坐标是隐私保护能力。
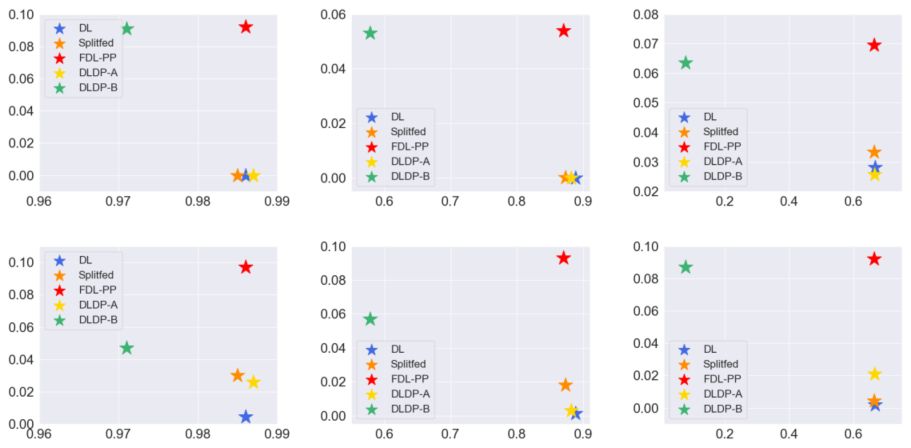
我们能很直观地感受到,FDL-PP方法在模型准确率与隐私保护性能两方面均占上风。
作者还给出了各种隐私保护方式在各条件下的详细数据表格,如下所示。
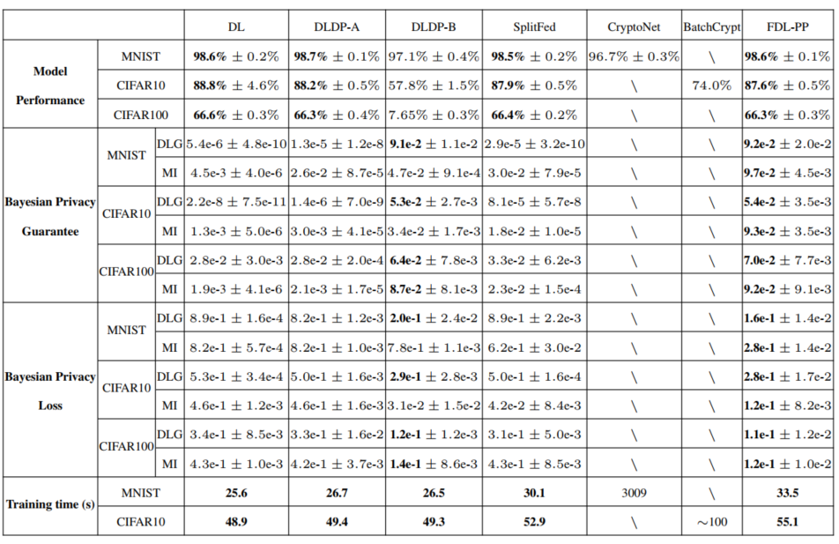
可以发现,相对于除同态加密之外的算法,FDL-PP的训练速度并没有优势,但也在可用的范围内。而基于同态加密的算法其所需训练复杂度有些难以接受。
综合上述实验结果,我们可以得出结论,在可用的训练复杂度范围内,FDL-PP方法在模型准确率与隐私保护性能上相对其他方式有明显优势,因此,确实是一种有效的改进方法。
实验性验证
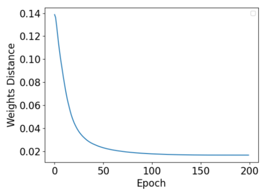
还记得在理论分析部分中,作者用到了三个假定来支持其结论,而这三个假定难以通过理论分析进行论证。因此,作者为三个假定分别设计了验证性的实验,结果如下:
- 假定一:没有passport层时,不同参与方之间的private模型通常会学习到较为相近的权重。
- 假定二:嵌入passport会使得scaling factor减小。
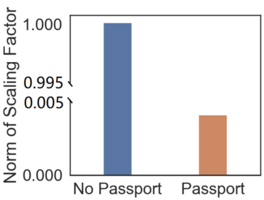
- 假定三:嵌入passport会使得参数的秩降低。
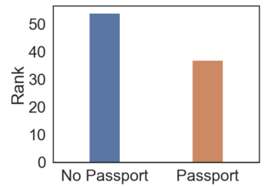
总结
本文主要算法FDL-PP是对split learning与前作中提出的passport方法的结合,方法上并不是从0到1的创新,但实际效果确实较为优秀。
本文对于隐私保护能力的评估体系Bayesian Privacy看似复杂、高大上,但只停留在理论阶段,到最后经过层层简化,也不过是对还原出的图像与原图计算一个MSE loss,说明成熟且实用的隐私保护能力评估体系设计确实有难度。因此差分隐私体系受到追捧也不是没有道理的,其自成体系的逻辑可以为相关的分析带来许多便利,并且能够使得理论为大家所接受。
文章对于隐私保护方式、攻击方式以及隐私保护评估体系的形式化做得较好,值得学习借鉴。
文章的理论推导过程中用到一些经验性的结论难以通过推导直接得出,因此转而对这些结论进行实验性的检验与说明,这样的做法也很值得借鉴。
总的来说,无论是从研究上还是写作上,本文都是一篇很有价值的文章,值得学习借鉴。在组会上进行分享时,本文也引起了老师与同学的广泛讨论,促进了实验室成员相互之间的深度交流。这也是本人在组会上分享文章时第一次获得大家如此热烈的反响,体验极佳🥰🥰,也让本人深刻体会到阅读与分享好文章所带来的收获感与成就感。
最后修改于 2021-10-26